
東京画廊の山本豊津代表と知り合って、画廊に伺って何回目かの時に
「あなたは絵画を音楽のようにしたいといいますが、それなら僕は、音楽は音楽、絵画なら絵画を観るな!」
と言われ、返答に窮してしまったことがあります。
でも、やはり絵画と音楽を融合することは重要であると確信していました。
この意見に、どう答えるべきだったのかを今日は解説しましょう。
時代を画するようなアイデアは異なるものの新しい組み合わせだ。
これは、数十年前から広告代理店の社員などが認識して利用して来た、良いアイデアを出すための鉄則です。
こちらの『アイデアのつくり方』というサイトで、この鉄則を最初に本にして世に知らしめたジェームス W.ヤングが、『素晴らしいアイデアのひらめき方』を解説しています。
実は、ヤングの本は、もう30年も前に読んでいたのですが、その意味をハッキリと充分に理解したのはここ数年のことです。
それは、経営する札幌WEBプログラミングスクールの小中高校生コースでほぼ全員に創造力育成講座『良いアイデアの出し方』の授業を行っており、講座内容を考えて生徒に教えるなかで、あらためて鉄則の意味を深く理解したからです。
ヤングは著書の中で、
「時代を画するような素晴らしいアイデアは、それまで異なるもと考えられていたものに共通する法則を見つけ出し結合した新しい組み合わせである。」
と提唱しました。
どうです?よく意味が分かりませんか?
具体的な例を挙げましょう。
天才スティーブ・ジョブズは世界で初めてスマホを販売しましたが、これはパソコンと携帯電話を組み合わせたものですよね。
それまで、世界では日本製の携帯は多機能すぎて、世界で孤立した時代遅れのものという意味でガラケーと呼んでいましたよね。
実はこの時も、何人かの物事の良く分かった人はNTTに言って「スマホを作ってください」と頼んだのですが、社員はいつも「それは無理ですって。どれだけ技術的に難かしいのか分かってください!」と言って断ったのです。
実際、ジョブズは「iphoneの発売までに1000の技術的な難題を解決しなくてはならなかった」と言っています。
アンパンがありますよね。これも日本のアンと西洋のパンを組み合わせたもの。
自動車は馬車にエンジンを組み合わせたもの。
カメラは暗箱にレンズとシャッターを組み合わせたもの。
ミュージカルは演劇と音楽の講演を組みあわせたもの。
ビートルズやローリングストーンズのロックミュージックはクラッシック音楽と黒人音楽、リズム&ブルースを結合したもの。
どうです?まさしく異分野の組み合わせから素晴らしいアイデアは生まれていますよね。
ポアンカレは「数学とは異なるものを同じと見なす技術である」と考えて幾何学と代数学を結合して位相幾何学を作った。
ポアンカレは「数学とは異なるものを同じと見なす技術である」と定義しました。
こちらのABC予測を解いたという望月教授に関する解説をしたNHKの番組サイト『数学者は宇宙をつなげるか?ABC予想証明をめぐる数奇な物語』にその分かりやすい説明が載っています。
「そもそも数学は、違うものを同じと見なすことで誕生したといわれています。例えば、リンゴが三つと、杭に3回まかれたロープ。この二つは全く異なるものです。しかし人類は、歴史が始まるはるか前に、この二つに「全く同じだ」と思える共通点を見つけ出しました。そう、「3」という抽象的な概念の発見です。数学はこうして始まったと考えられているのです。」
トポロジーとはどういうものか?
簡単に言うと、正方形や球といった立体の体積や面積を求める式はありますよね。
では、コーヒーカップや船、メガネフレームの体積を求める式はどうでしょう?ありますか?
ポアンカレ以外の数学者はこれを無理と考えたのです。
しかし、ポアンカレは『同じ形式の立体(幾何)は、数式(代数)で表せる』ことを発見し、その方法を確立したのです。
もっと具体的に説明しましょう。
同じ形式=タイプとは何か?これを数学の世界では位相と呼びます。
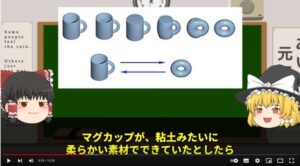
位相とは、穴が一つある図形、つまりドーナツとコーヒーカップは同じ位相であるというのです。これは粘度細工でドーナツをコーヒーカップに変形できるからです。
そこで、ポアンカレはドーナツの体積などを表す式を発見し、この式を変形・操作することでコーヒーカップを表す式を作ったのです。
では、この事の何が画期的なのか?
私はこれについてはそれ程詳しくないのですが、恐らく世界で初めてそれまで数式で表せなかった立体を数式で表現できるようになったことです。
そうすると飛行機の機体の一部分や部品も数式で表し、正確に製造できるようになったのではないでしょうか?
現に旅客機の設計では、より優れた材料により軽量化する場合の構造の最適化=形状設計なども効率的にできるようになりました。
また、モーフィングというコンピュータグラフィクスで、ある主人公などを人間から猿やロボットに変形させることもできるようになりました。
それまでは、翼の一部の曲線を式に表す事はできました。高校で習った微分方程式ですね。また体積を計算することも出来ました。積分ですね。
しかし、その立体そのものを表す数式を記述する扉をポアンカレが開いたように推測します。
ですから位相幾何学は画期的な発見で、これによって図形、立体を研究する幾何学と、数式を研究する代数学が結合したのです。
『音楽と絵画』に共通法則を発見して結合したのが私です
ポアンカレと同じ事を歴史上はじめて『音楽と絵画』で行ったのが私なのです。
ですから、最初の東京画廊の山本豊津さんの質問への答は
「異種と考えられた音楽と絵画の共通法則を発見して結合することが、表現の多様さや今までに無かった新鮮で斬新な表現を可能にする。」
ということですね。
以前にも何度かお話していますが、私は絵画が動かないこと、静止していることが高校時代から許せなかったのです。
絵画は正面から見た静止画像で死んでいるに等しいと思いました。
なぜ、画家は画面上の動きを追及しないのか?
音楽が持つ、時間とともに部分・パターンが繰り返さて変化するその力を取り込もうとしないのか?
以前に、これとまったく同じことを考えた画家がいます。
パウル・クレーです。彼はこう言いました。
「ベートーベンやモーツアルトの曲を演奏した後に、絵画を見ると苦笑せざるえない。」
「だからこそ今、私が絵画の音楽的な可能性を発見し発展させることが必要と感じたので私は画家となろうと思う。」
彼とバウハウスで同僚だったカンディンスキー以来、この認識を共有して継承した画家は私以外に一人もいません。
ですから、私は現代の絵の全てに不満なのです。
これは、今現在、ガコシャンやハウザー&ワースと契約している画家であることなどとはまったく無関係のことです。
これらの画家は画商が価値ありと考えているだけであり、動きの無いものはやはりつまらないのです。
もう一度繰り返しますが、私によって始めてこの音楽の力を絵画に取り込んで本格的に発展させる時代が来たのです。
フジテレビ『料理の鉄人』に見る異分野結合の威力
これも札幌プログラミングスクール小中高校生コースの『創造力育成 良いアイデアの出し方講座』で教材として使っているのですが、1995年から放映されたフジテレビの『料理の鉄人』という番組がありました。
毎週 TV局が探して来た挑戦者が番組の冒頭で3人または4人の鉄人の誰かを指名して、その日に局が指定した食材「例 牛肉」などを使用した料理を1時間で何皿か作り、審査員が審査して点数をつけ合計点の高かった人が勝者となる番組です。
主な鉄人は和食の道場六三郎、中華の陳健一、イタリア料理の神戸勝彦、フレンチの鉄人が坂井宏行。
鉄人の勝率はもの凄く高く道場六三郎は87%、フレンチの坂井宏行が80%、中華の陳健一が72%.
道場氏と酒井シェフの勝率が高いですが、この2人には共通する特徴があります。
それは 自分の料理のジャンルにとらわれず、多ジャンルの料理と自分の専門とする料理を結合させたことです。
道場さんはフォアグラなどフレンチの食材も使用し得意としており、坂井シェフは高名な料亭の吉兆に通いつめ、フレンチと和食を融合させ、懐石料理の盛り付けの美しさを取り入れたフレンチのパイオニアで、その繊細にして見事な盛り付けの料理で『フレンチのドラクロア』の異名を取りました。
坂井シェフはお菓子作りも得意でパテシエでないにもかかわらず、数々の腕利きパテシエとのお菓子対決で全勝しているはずです。
坂井シェフや道場さんの『異分野の結合』には、著名な料理評論家の山本益博さんなど料理界から邪道であるという強い非難がありました。
しかし毎回、バッタバッタと挑戦者を退けていく鉄人の姿は『異分野の結合』がいかに有利に働き威力を発揮するかということを顕著に示しているのではないでしょうか?
こちらに、料理界から邪道と非難されながら吉兆に通ったことなどを話している坂井シェフのインタビュー記事があります。
是非、ご覧ください。
札幌在住のパステル画家、横田昌彦のアートマガジンのご紹介です!
メールアドレスを登録するだけで、その日から次々とアートに関する、とても役に立つ情報をお届けいたします。
内容は美術作品の鑑識方法や投資も兼ねて購入するならどの作品が良いか?
ネットで美術作品を販売して高い実績を挙げている懇意にしている作家の販売方法情報など盛りだくさん!
ここ数年の、海外で最も高く評価されているアートは、アメリカの警察官による黒人暗殺事件や、伊藤詩織さんの強姦逮捕未遂事件に端を発した『Me Too 運動』、ウクライナやミャンマーなどの内紛事件、香港の民主主義弾圧などと表裏一体となる表現活動です。
中国のアイ・ウェイウェイや日本にも馴染みの深いドイツのヒト・シュタイエルといった作家が、世界で最も影響のあるアート・パーソンに選ばれています。
こういった世界最前線情報も分かりやすく知ることができますよ!
気軽に登録して、是非、読んでみて下さい!
皆さんのご登録を笑顔でお待ちしております!
◆ご登録は画像をクリックしてください!









